Rによる信号処理

Rについて

必要に迫られて，最近Rを使い始めました．授業においても使い始めましたので，授業用に作成したものをBlog用に編集しなおして掲載します．にわかRユーザですので，間違ったことを書いているかもしれません．

「R(The R Project for Statistical Computing: https://www.r-project.org/」は，統計解析及びグラフを表示させるための言語及びその開発環境です．統計解析ソフトには他に，SPSSやSASなどがありますが，Rは無償のソフトウェアで，配布サイトCRAN(The Comprehensive R Archive Network: http://cran.ism.ac.jp/ ※2025/07/10現在リンク切れ)にて，Linux版，(Mac) OS X版，及びWindows版，それぞれ取得可能です．

Rの基本的な使い方

Rを起動すると，ターミナル（コマンドプロンプト）のような画面が表示され，最下行に「>」のプロンプトが表示されます．これはユーザからのコマンドの入力を待機している状態です（図1）．この辺はGnuplotやOctaveなんかと一緒ですね．

図1 RGui Windows版.

終了方法は，「q()」と入力しEnterか，Windowsの場合は閉じるボタンで終了することができます．

Rは，RubyやPerl等と同様プログラミング言語ですので，条件分岐（if）や繰り返し（for）等の構文が使用できます．変数（Rでは「オブジェクト」という）への代入については，「<-」（他の言語同様「=」も使用可能）を使用します．

> a <- 1 + 3 * 5
> a
[1] 16 

変数（オブジェクト）名等には日本語も使用することができます．Rでは，これらオブジェクトをベクトルとして扱います．例えば，1×5のベクトル [1, 2, 3, 5, 7] のようなオブジェクトを作成する場合は，ベクトル作成関数「c()」を用いて，次のようにコマンド入力します．

> x <- c(1, 2, 3, 5, 7)
> x
[1] 1 2 3 5 7 

他に，交差1の等差数列の規則的なベクトルを生成する場合は次のように実行します．

> y <- 1:5
> y
[1] 1 2 3 4 5 

もちろん，ベクトルの加算や乗算等の演算も可能です．コマンド全体を括弧で囲むと，代入結果も表示されます．

> c <- x + y
> c
[1] 2 4 6 9 12

> (x2 <- x * 2)
[1] 2 4 6 10 14 

ベクトルの結果をグラフ化したい時は，plot()関数を使用します．ベクトル x をプロットするときは「plot(x)」とコマンドを実行すればいいだけです．plot()関数には様々なオプションがあり，軸の範囲やラベル，凡例を設定すると次のようなグラフ（図2）を描くことができます．

> plot(x, pch=2, type='o', xlim=c(0,6), ylim=c(0,8), ylab='Vector x', col='blue', lwd=2)
> legend('topleft', legend='Vector x', lty=1, lwd=2, pch=2, col='blue')

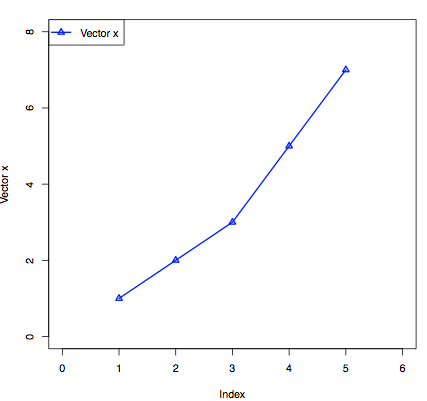図2 plot結果.

各オプションについては，ヘルプ「help(plot)」で参照可能です．

グラフをEPS画像（例「sample.eps」）として保存する場合は，次のコマンドで行います．

> dev.copy2eps(file='sample.eps')

Windowsの場合は，グラフのウインドウ内でショートカットメニュー（右クリック）で，「ポストスクリプトに保存…」を選択します．楽ちんですね．

基本的な信号処理

合成波信号の周波数解析（離散フーリエ変換）

次のような課題をRで行ってみます．

振幅が1で周波数10[Hz]の正弦波と，振幅が1/4で周波数30[Hz]の余弦波の合成波信号データについて，離散フーリエ変換（FFT）によって得られた振幅スペクトルを取得しなさい．ただし，サンプリング周波数FSは160[Hz]，標本間隔DTは6.25[ms]（1/FS），標本の個数Nは16個とする．

sin関数，cos関数については，それぞれ sin()，cos() を使用します．フーリエ変換（FFT）については，fft() 関数を使用します．fft() は，複素数（cplx）型を返すので，プロットする際は，Mod() にて絶対値，あるいは Re() で実部，または Im() で虚部，それぞれのベクトルを指定すれば良いでしょう．

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
FS <- 160                     # サンプリング周波数 FS=160[Hz]
DT <- 1/FS                    # 標本間隔 DT=1/160=0.00625[s]
N <- 16                       # データ数 N=16
i <- 0:(N-1)                  # 添字(index)の範囲 i
 
##### 振幅1，10[Hz]の正弦波(siga)
siga <- sin(2*pi*10*DT*i)
plot(siga)
plot(DT*i, siga, xlab='Time', type='o')    # plotして確認
 
##### 振幅0.25，30[Hz]の余弦波(sigb)
sigb <- 0.25*cos(2*pi*30*DT*i)
plot(DT*i, sigb, xlab='Time', type='o')    # plotして確認
 
##### 合成波(sig)
sig <- siga + sigb
plot(DT*i, sig, xlab='Time', type='o')     # plotして確認
 
spec <- fft(sig)/N                # FFTの実行
 
plot(abs(spec),type='h')         # 絶対値のスペクトル
plot(Re(spec),type='h')          # 実部値のスペクトル
plot(Im(spec),type='h')          # 虚部値のスペクトル
 
plot(Re(spec),type='h',col='blue', ylab='', ylim=c(-1,1))
par(new=T)                       # グラフを上書き可能モードにする
plot(Im(spec),type='h',col='red', ylab='Spectrum Xk', ylim=c(-1,1))

合成波信号の波形及びそのFFT結果を図3に示します．

0.1[s]=DT*16=0.00625*16 を基本波の周期としますので，その逆数である10[Hz]が基本波の周波数となります．k=1の場合が基本周波数ですので，k=3が30[Hz]を意味します．k=1の時に虚部のところにスペクトルが現れるのでsin成分を示し，k=3の時は実部に現れるのでcos成分を示します．k=1に対してk=15，k=3に対しk=13と，ちょうどk=8を折り返し周波数として対象的に現れます．

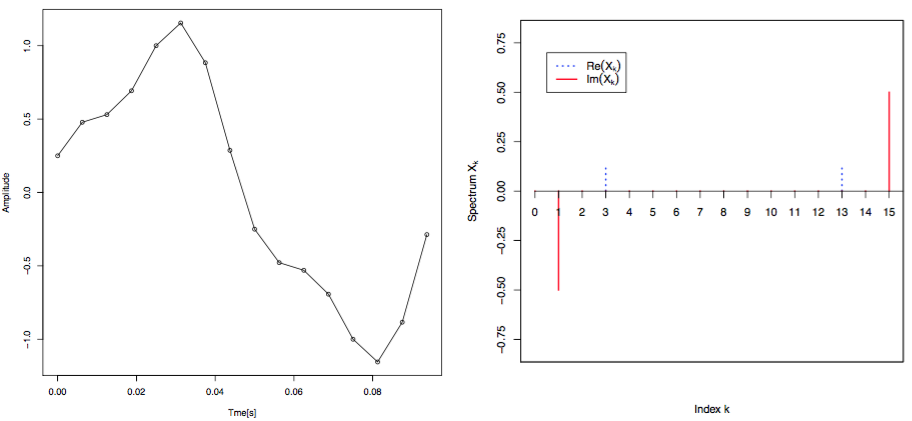図3 合成派の信号波形とそのFFT結果.

FFT結果のグラフについては，実は上記コマンドだけでは表現が足らず，実際は axis() 関数等を用いて，グラフの出力に工夫しています．

1
2
3
4
5
6
7
plot(i, Re(spec), type='h', xaxt='n', yaxt='n', col='blue', lty=3, lwd=2, ylim=c(-0.8,0.8), ylab='', xlab='')
par(new=T)
plot(i, Im(spec), type='h', xaxt='n', yaxt='n', col='red', lty=1, lwd=2, ylim=c(-0.8,0.8), ylab=expression(paste('Spectrum ', X[k])), xlab='Index k')
axis(1, pos=0, at=0:16, adj=0)
axis(2, at=seq(-1, 1, by=0.25))
 
legend(0.5, 0.7, legend=c(expression(Re(X[k])), expression(Im(X[k]))), lty=c(3,1), col=c('blue', 'red'), lwd=c(2,2))

外部データファイルを利用する場合

入力信号データとして，外部ファイル（テキスト形式ファイル）を用いる方法について説明します．次のような入力データファイル「rect.dat」を準備し，これを入力信号データとして，この信号のFFTの結果を取得します．

1.0
1.0
1.0
1.0
1.0
1.0
1.0
1.0
-1.0
-1.0
-1.0
-1.0
-1.0
-1.0
-1.0
-1.0

実際にテキストファイルを読み込んで，テーブルデータのオブジェクトとして格納し，FFTの結果を表示させてみます．

現在のディレクトリの確認と，ファイル「rect.dat」があるディレクトリへの移動（セット）

> getwd()
> setwd("C:/Users/hogehoge/Desktop")

ファイル「rect.dat」の読み込み

> N <- 16
> x <- read.table("rect.dat")

データを表示させてみる

> x[9, 1]
[1] -1

> x[,1]
[1] 1 1 1 1 1 1 1 1 -1 -1 -1 -1 -1 -1 -1 -1

FFTの実行，結果の実部だけを表示させてみる

> y <- fft(x[,1])/N

> df <- data.frame(ak=Re(y), bk=Im(y))
> df$ak

dfの出力結果が次のようになります．

      ak         bk
   0.000    0.00000000
   0.125   -0.62841744
   0.000    0.00000000
   0.125   -0.18707572
   0.000    0.00000000
   0.125   -0.08352233
   0.000    0.00000000
   0.125   -0.02486405
   0.000    0.00000000
  0.125    0.02486405
  0.000    0.00000000
  0.125    0.08352233
  0.000    0.00000000
  0.125    0.18707572
  0.000    0.00000000
  0.125    0.62841744

音声データの信号解析

次に，実際の音声信号データを周波数解析してみます．Rには音声データ等を扱うパッケージも用意されています．ここでは，「tuneR(https://cran.r-project.org/web/packages/tuneR/」というパッケージを使用します．パッケージがインストールされていない場合は，次のコマンドでインストールが可能です．

> install.packages("tuneR") 

場合によっては，CRANミラーサイトを選択するようダイアログが表示される場合があります．その場合は，CRANミラーサイトのリストから，「Japan(Tokyo)」または「Japan(Tsukuba)」を選択します．パッケージをインストールしたら，次に，「tuneR」のライブラリを利用できるよう次のコマンドを実行します．

> library(tuneR) 

例として，440[Hz]の正弦波信号（音声信号）を生成し，それを実際にプレーヤーを使って音を流してみます．

> beep <- sine(440)
> play(beep) 

Windowsの場合は，デフォルトで，Windows Media Playerが実行されます．

それでは，この音声信号の波形と，周波数解析（FFT）した結果を表示させてみます．

1
2
3
4
beep <- sine(440)
plot(beep@left, type='l', xlab='Time', xlim=c(0,1000))
spec_beep <- fft(beep@left)
plot(abs(spec_beep),type='h', xlab='Frequency', xlim=c(0,1000))

音声データ（WAVEデータ）は左右2つのチャネルで構成されているので，左チャネルだけのデータ「beep@left」を利用します．

図4 SIN波（440[Hz]）の音声信号波形とそのFFT結果.

> mywave <- readWave("sample.wav")
> play(mywave)
> spec <- fft(mywave@left) 

実際に，ドラムスのシンバル（ハイハット）の音と，バスドラのキックの音を解析した結果を図5に示します．X軸（Frequency）の範囲を限定していないので，折り返しの周波数成分も表示されていますが，バスドラの方は低音域に，シンバルは中〜高音域にスペクトルが集中して現れているのがわかります．

ちなみに使用した音声ファイルは，下記サイトより拝借いたしました．（深謝）

出典: 音の博物館～Sound material room～

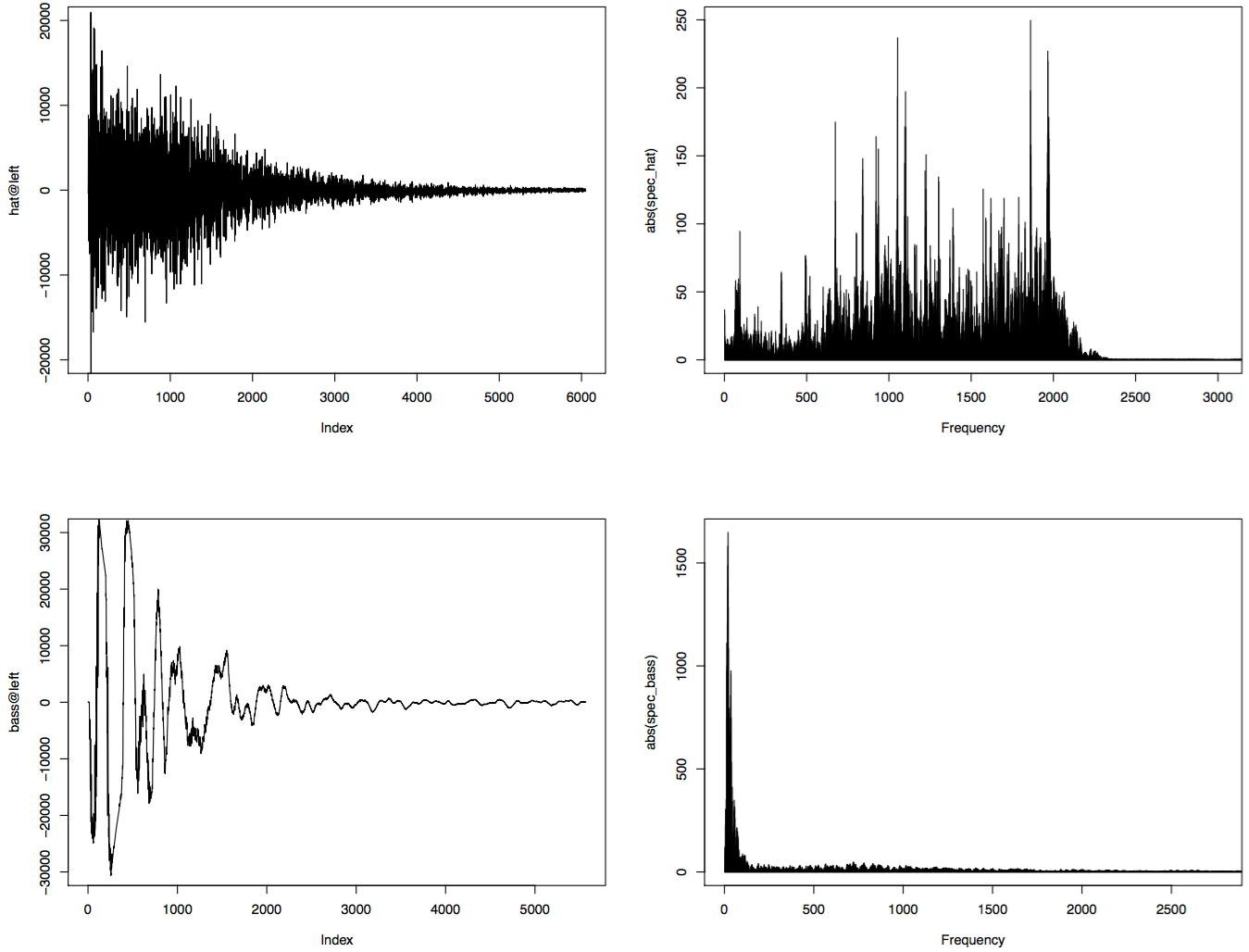図5 シンバル（ハイハット）音の信号波形（左上）とそのFFT結果（右上），バスドラのキック音の信号波形（左下）とそのFFT結果（右下）.

参考サイト

R-Tips ※2025/07/10現在リンク切れ
統計解析フリーソフトRの備忘録 ※2025/07/10現在リンク切れ
An Introduction to R